Le format JPEG

J.P.E.G. sont les initiales de Joint Photographic Experts Groups, le groupe qui a créé ce format en 1987. J.P.E.G. est un format d’image très utilisé notamment dans le codage de vidéos M.P.E.G. (Moving Photographic Experts Groups). Ce format a l’avantage de fournir des images de bonne qualité et de petite taille, donc particulièrement utile sur Internet. En plus il permet de choisir quelle qualité d’image on veut obtenir, sachant que plus la qualité est faible, plus la taille de l’image est faible. Cette compression est donc une compression avec pertes.

I. Fonctionnement général du J.P.E.G.

Le codage J.P.E.G. s’effectue en plusieurs étapes :

La perte de qualité s’opère principalement pendant la quantification, la saturation et le downsample.

Le décodage s’effectue également en plusieurs étapes

Nous allons maintenant voir les différentes étapes du codage J.P.E.G. en détail.

II. Le passage de RGB à YCbCr et le downsample

1. Le passage des composantes RGB en composantes YCbCR

Habituellement, les images sont stockées avec les composantes RGB (Red Green Blue :Rouge Vert Bleu). Or le système RGB n’est pas le mieux adapté pour appliquer le codage J.P.E.G. car l’œil humain est plus sensible à la luminance (ou luminosité) qu’à la chrominance d’une image. Or la luminance est présente dans les trois couleurs rouge, vert , bleu. Ainsi on transforme les composantes RGB de l’image en une composante de luminance notée Y et en deux composantes de chrominance notées Cb et Cr. Pour cela on utilise des formules de passage (pour un pixel) :

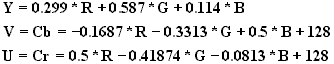
On obtient facilement les équations pour le passage des composante YCbCR aux composantes RGB :

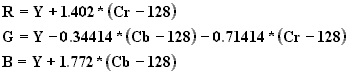
Cette transformation des composantes RGB en composantes YCbCR est bijective. Ainsi il n’y a pas de pertes de données pendant cette étape.

2. Comment a-t-on obtenu ces coefficients?

On a tout d'abord commencé par fixer les coefficients pour Y la luminance. La luminance est une quantité physique objective. La luminance (parfois appelée brillance) est définie par l'intensité de la radiation lumineuse par unité de surface émettrice. La luminance est conservée lors du passage de l'image couleur à l'image noir et blanc. Donc, il est facile de déterminer ces coefficients, ce qui donne: Y=0.3*R+0.59*V+0.11*B.

On a mesuré les coefficients et on a normalisé en supposant que la valeur 255 (valeur maximale) était la luminance du blanc. Cette mesure est effectuée par des récepteurs photoélectrique: on fait les mesures pour le rouge, le vert, le bleu et on divise par la somme des trois résultats. Ainsi on obtient les coefficients donnés au dessus.

Ensuite, on en déduit les deux coefficients U et V (ou Cr et Cb). En effet, on va imposer pour U et V quelles soit respectivement dans le plan (R,Y) et dans le plan (B,Y) (ce qui revient à mettre R dans le plan (Y,U) et B dans le plan (Y,V)). Ainsi on pose U de la forme: U=a*(R-Y) et V=b*(B-Y). Cette forme de U et V permet à U et V d'être orthogonales ainsi on obtient une base orthogonale comme la base RVB. Cependant, il reste à fixer les coefficients a et b. On peux choisir arbitrairement le coefficients a et b. La formule donnée au paragraphe précédent utilise des coefficients a et b et une addition (+128) pour que les deux composantes Cb et Cr restent comprises entre 0 et 255. Dans ces formules le coefficient a = 0.713 et b = 0.565 ceci permet aux composantes Cb et Cr de rester entre 0 et 255 (après arrondis). En effet pour Cb: 0.1687 + 0.3313 = 0.5 donc quelque soit R, G, B, Cb est compris entre 0 et 255. De même pour Cr.

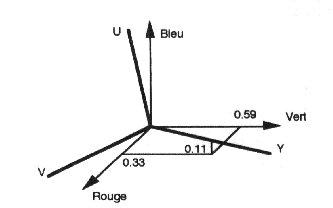
Passage du système de couleurs RVB au système YUV

3. L’étape de downsample (sous échantillonnage)

On a vu que l’œil est moins sensible aux composantes de chrominance. Ainsi une perte de donnée sur les deux composantes de chrominance à peu d’effet visible sur l’image. Ainsi on effectue sur ces deux composantes l’étape du downsample, c’est à dire que l’on va transformer les matrices 8 x 8 en matrices 4 x 4. Pour cela on prend quatre cases de la matrice (deux cases horizontales par deux cases verticales) . Ensuite on fait la moyenne de ces quatre cases. Ainsi on obtient une matrice 4 x 4. On a ainsi diminué la taille des deux composantes de chrominance par quatre et donc globalement on a diminué la taille de l’image par deux sans changements visibles de l’image.

Pour l’étape inverse , il suffit de prendre une case de la matrice 4 x 4 et de remplir quatre cases de la matrice 8x8 par la valeur de cette case. On voit donc que cette étape n’est pas bijective et donc qu’elle entraîne une perte de données mais ces pertes ne sont pas visibles.

On peut vérifier que l'on peut négliger les composantes de chrominance par un exemple. (la photo originale est affichée plus bas pendant l'étape de la DCT)

composante de luminance (chrominance fixée à 128) composante de chrominance (luminance fixée à 128)

Image 1: Composante de luminance (chrominance fixée à 128)

Image 2: Les deux composantes de chrominance (luminance fixée à 128)

III. Les transformations D.C.T. et I.D.C.T.

1. D.C.T.

La D.C.T. (Discrete Cosine Transform) est une transformée de Fourier dont on a remplacé les sinus par des cosinus. On peut interpréter la D.C.T. comme une transformation prenant en entrée un signal (constitué dans le cas du J.P.E.G. de 64 pixels) fonction des dimensions spatiales x et y. La D.C.T. décompose ce signal en 64 signaux. Chaque signal contient une fréquence spatiale. La D.C.T. donne l’amplitude de ces signaux.

Soit n(i, j) les coefficients de la matrice où est stockée la partie de l’image à traiter, avec (i,j)ÎO0,7P², et soit F(u, v) les coefficients de la matrice obtenue après la transformation D.C.T. , avec (u,v)ÎO0,7P². Ainsi les indices commencent à 0 et non pas à 1. La formule de la D.C.T. est :

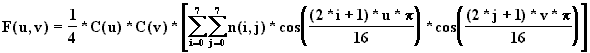
Avec C(x) = 1/sqrt(2) si x=0 sinon C(x)= 1.

On voit que le calcul d’un coefficient demande 8*8=64 additions. C’est pour cette raison que l’on utilise des matrices 8x8. En effet si on prenait la matrice de l’image entière alors une petite image de dimension 100x100 demanderait 10000 additions pour le calcul d’un coefficient. On constate donc que la transformation D.C.T. serait très longue si l’on n’utilisait pas des matrices 8x8.

2. I.D.C.T.

L’ I.D.C.T. est la transformation inverse de la D.C.T. Pour les mêmes raisons que pour la D.C.T., elle s’applique à une matrice 8x8. La formule de l’ I.D.C.T. est :

3. Comment obtenir une DCT plus rapide ?

L'idéal serait de faire la DCT sur toute l'image, cependant, cela prendrait un temps très long. En effet, si la longueur et la largeur de l'image sont de N, le calcul de la DCT est en N^4 ce qui devient rapidement incalculable dans un temps convenable. Pour éviter cela, on fait le calcul de la DCT en bloc. C'est à dire que l'on applique la DCT sur un bloc de longueur fixe. La taille idéal du bloc est de 16x16. En effet, au delà de 16 pixels, les pixels n'ont que peu de relation entre eux. Ainsi on pourrait faire la DCT sur des blocs plus gros mais on ne gagnerait pas grand chose, ni en qualité, ni en taille. Cependant, la taille a été fixée à 8x8 par le groupe qui a créé le JPEG. Ce choix donne également de très bon résultats.

On peut facilement accélérer la DCT en ne calculant qu’une seule fois le produit des deux cosinus. En effet, il n’y a que 64 combinaisons possibles pour le couple (u,v) donc il suffit de calculer au départ les 64 valeurs possibles, les stocker dans un tableau et ensuite, on ne les calcule plus. Ceci est très important car la DCT est l’opération qui coûte le plus de temps dans le codage JPEG.

4. Avantages de la D.C.T. sur la F.F.T.

a. Généralités sur les transformées

La DCT et la FFT font partie de la même classe de fonctions mathématiques : ces fonctions prennent un signal de base et le transforment d’une représentation à une autre.

Contrairement à la FFT qui prend un signal en deux dimensions, la DCT prend un signal en trois dimensions : X et Y sont les deux dimensions de l’image, et Z est la couleur (ou la valeur du pixel). Après la DCT, il y a 64 valeurs donc autant que précédemment. Ainsi, on peut se demander ce qu’on a gagné à faire cette transformée par rapport à la FFT par exemple ou même, on peut se demander si faire une transformée est bien utile.

On remarque que plus on s’éloigne de l’origine et plus les fréquences correspondantes sont élevées. Or la plupart des images sont composées d’informations de basses fréquences. Donc quand on s’éloigne de l’origine, on trouve des coefficients faibles et qui en plus sont peu importants pour la vision. Ainsi la force de la DCT est de "choisir" les éléments importants de l'image (ce qui semble difficile à faire sur une image non transformée). Donc on voit l'utilité de faire une transformée

b. Fonctionnement de la F.F.T

La formule de la F.F.T. est assez proche de celle de la D.C.T. :

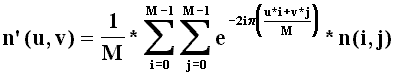Avec dans le cas des matrices 8x8 M=8

La réciproque est:

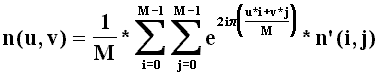
Ainsi en appliquant la FFT, on obtient deux matrices (une matrice de la partie réelle et une matrice de la partie imaginaire). On peut penser que la FFT nous a doublé la taille des données. En fait ce n'est pas le cas car on remarque que (on travaille dans le cas des matrices 8x8):

Ainsi, dans les deux matrices réelles et imaginaires, il y a des cases qui ont toujours la même valeur. Ainsi, il suffit d'avoir ( en remarquant que les cases (0,0) (4,0) (0,4) (4,4) de la matrice imaginaire sont toujours nulles) :

	0	1	2	3	4	5	6	7
0
1									cases à garder pour la matrice réelle
2
3									cases à garder pour la matrice imaginaire
4
5
6
7

Ainsi, il est possible d'utiliser la transformée de Fourrier sans augmentation de taille.

c. D.C.T. vs F.F.T

Bien qu'étant plus longue à calculer que la FFT, la DCT comporte certains avantages. En effet, la DCT n'utilise pas de coefficients complexes, ceci rend la programmation légèrement plus simple. Cependant, la FFT renvoyant 64 coefficients complexes semble doubler la taille des données (64 coefficients complexes = 128 coefficients). En fait la taille des données n'est pas doublée car il y a des redondances prévisibles. Ainsi cela ne représente qu'un faible avantage.

Mais il y a un avantage bien plus grand qui est le fait que la DCT repartit l'énergie du signal sur une bande de fréquences plus basses que la FFT et donc il y a moins de coefficients importants que pour la transformée de Fourier. Donc si on néglige les petits coefficients dans la FFT, on aura une perte très grande. C'est pour cela que l'on utilise la FFT.

Cet avantage de la DCT est due au fait qu'avec la DCT, on observe le signal sur une période 2*N contre N pour la FFT. Cela se voit sur les formules de passage entre DCT et FFT: pour une suite x(n):

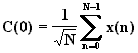
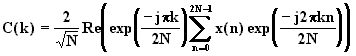pour 0<k<N. Avec N le nombre d'échantillons (8 pour le JPEG).

Ainsi comme le calcul se fait sur une période 2*N, alors l'énergie du signal se trouve dans des fréquences plus basses et donc on a besoin de moins de coefficients.

Exemple d'une rampe:

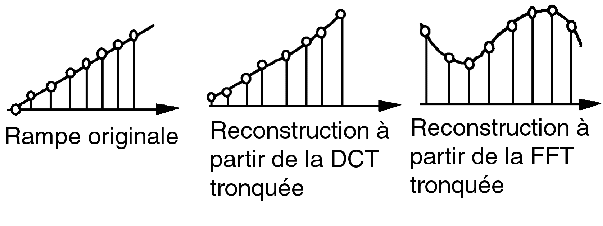
Donc on voit clairement (avec cette expérience) que la reconstruction à partir de la DCT donne de bien meilleurs résultats qu'avec la FFT.

On peut également pour voir la différence entre la DCT et la FFT appliquer l'algorithme entier du JPEG sur une image, en utilisant dans un cas la FFT et dans l'autre la DCT, sans rien changer d'autre.

Image de départ (292 Ko)

Image avec FFT (Fq=0, Taille = 107 Ko)

Image avec FFT (Fq=3, Taille = 22 Ko)

Image avec DCT (Fq=3, Taille = 25 Ko)

Ainsi, on remarque que la FFT peut être utilisée pour le JPEG (Si on met le facteur de qualité à 0, on remarque que l'image finale est de bonne qualité). Cependant, si l'on utilise la FFT, on est obligé de garder de petits facteurs de qualité et donc d'obtenir une faible compression (on a divisé par 3). En effet, on voit nettement que l'image avec un facteur de qualité trois est fortement détériorée, ce qui n'est pas le cas de la DCT.

IV. La quantification et la déquantification

Cette étape est la principale étape de perte de données. En effet le principe de la quantification est de créer une matrice de quantification et de diviser chaque terme de la matrice obtenue par la D.C.T. par son terme correspondant de la matrice de quantification. Soit F(u,v) les coefficients de la matrice obtenue après la D.C.T. et a(i,j) les coefficients de la matrice de quantification, avec (u,v,i,j) ÎO0,7P⁴. Soit b(k,l) les coefficients de la matrice obtenue après quantification, avec (k,l) ÎO0,7P². Alors b(k,l)=E(F(k,l)/a(k,l)), avec E(x) la partie entière de x.

Après la D.C.T. , les fréquences élevées sont dans le coin droit du bas de la matrice. Or l’œil humain discerne mal ces fréquences. Ainsi la manière la plus astucieuse de créer la matrice de quantification est de mettre des valeurs faibles dans le coin gauche du haut et des valeurs fortes dans le coin droit du bas.

En fait, on peut utiliser plusieurs formules plus ou moins simples pour la matrice de quantification. Par exemple la formule suivante est simple et donne de bons résultats :

Avec Fq le facteur de quantification et T une constante (par exemple 1).

On voit que cette formule donne bien des valeurs fortes dans le coin droit du bas et des valeurs faibles dans le coin gauche du haut de la matrice.

Après la quantification, il y a une étape de saturation pour que chaque valeur obtenue dans la matrice puissent être stockées sur un octet. Cette saturation s’effectue sur toute la matrice exceptée la première case de la matrice qui est proportionnelle à la moyenne de la matrice. Cette case est donc très importante ainsi on la stocke sur plusieurs octets. Cette saturation entraîne des meilleurs résultats sur des images contenant beaucoup de couleurs. En effet appliquer le codage J.P.E.G. sur une image en noir et blanc donne de très mauvais résultats car l’algorithme de la D.C.T. donne des valeurs très élevées pour une image en deux couleurs et donc la saturation entraîne une perte importante d’informations.

V. La compression

Après la D.C.T. et la quantification l’image n’a pas été réduite. C’est donc pendant la phase de compression que l’on va obtenir un gain de place.

1. Le codage R.L.E.

Le codage R.L.E. (Run Length Coding) est une méthode de compression très simple. Son principe est de remplacer une suite de caractères identiques par le nombre de caractères identiques suivi du caractère. Par exemple AAAAAAA sera remplacer par 7A. Ici comme dans la matrice issue de la quantification il y a beaucoup de 0, on va appliquer le codage R.L.E. aux 0. Ainsi il faut obtenir les suites de 0 les plus longues possibles. On va donc lire la matrice en zigzag.

En effet, comme il y a beaucoup de 0 dans le coin droit du bas de la matrice , cette méthode va donner une suite de 0 assez longue.

2. Le codage Huffman

Le codage Huffman du nom de son concepteur est une méthode statistique de compactage. Son principe est de remplacer un caractère par une suites de bits, sachant que plus la probabilité d’apparition du caractère est forte et plus la séquence de bits représentant ce caractère sera courte. Plus précisément soit X1=(x₁...x_n) des symboles et (p₁....p_n) la probabilité d’apparition de ces symboles dans une séquence. Ainsi . Soit x_i0 et x_i1 les deux symboles qui ont la plus faible probabilité d’apparition. On étiquette les deux symboles x_i0 et x_i1 respectivement par 0 et 1. On crée un nouvel ensemble de symboles qui sont les n-2 symboles différents de x_i0 et de x_i1 affectés de leur probabilités, et un nouveau symbole qui a une probabilité de p_i0 + p_i1. Ainsi on obtient un ensemble de symboles de cardinal n-1 et un ensemble de probabilités de même cardinal. On peut donc appliquer de nouveau cet algorithme jusqu’à ce qu’il ne reste plus qu’un seul caractère de probabilité 1.

Ainsi grâce à cet algorithme on a constitué une table qui à tout symbole fait correspondre une séquence de 0 et de 1. En plus à un symbole qui a une forte probabilité correspond une séquence courte. La taille de la séquence augmente quand la probabilité diminue.

Pour illustrer le codage Huffman, on peut prendre un exemple :

Symbole

x₁

x₂

x₃

x₄

x₅

x₆

Probabilité

0.15

0.08

0.5

0.04

0.17

0.06

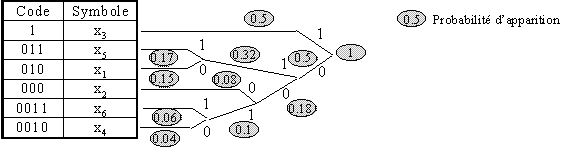
On obtient avec cet algorithme un arbre binaire et donc le décodage s’effectue très simplement en suivant l’arbre. Car une des branches correspond à 0 et l’autre à 1, et les feuilles sont les symboles. Ainsi ce codage est un codage bijectif et donc sans perte. Mais le codage Huffman ne permet pas toujours de réduire la taille des données car il faut stocker la table de conversion.

Conclusion

Le codage Huffman étant un codage à taille variable, l’erreur de transmission d’un des caractères peut entraîner une erreur sur toute la fin du fichier. Ainsi le format J.P.E.G. est un format très sensible aux erreurs. Il est donc préférable de ne pas l’utiliser quand le mode de transmission n’est pas sûr.

Bibliographie

La réduction de débit en audio et vidéo - John Watkinson ed. Eyrolles

Mathématique pour la physique - Pierrette Benoist-Gueutal, Maurice Courbage ed. Eyrolles

Technique de compression des images - Jean Paul Guillois ed. Hermès

Algorithmique combinatoire - Gérard Lévy ed. Dunod

Techniques de compression des signaux - Nicolas Moreau ed. Masson

Encyclopedia of Graphics File Formats - James D. Murray, William Vanryper ed. O’Reilly

La compression des données - Mark Nelson ed. Dunod

Modélisation d'images fixes et animées - J.P. Gourret ed Masson

Sites Internet :

http://www.sda.epita.fr/dossiers-HTML/tcom96/telecom/mpegjpeg/mpegjpeg.doc.html

http://www.geocities.com/Area51/chamber/9196/tsld014.htm

http://www.uni_duisburg.de/FB9/NGA/mitarbeit/burck/kompen/luma.htm

http://www.eleves.ens.fr:8080/tuteurs/cours/images/images_1.html

http://www.inforamp.net/~poynton/ColorFAQ.html

Pour des raisons de vitesse de chargement, les images affichées sont au format .jpg. Ainsi des erreurs supplémentaires peuvent apparaitre à cause de cette compression. Les images au format BMP sont téléchargeables: ici .

Page principale

Symbole	x₁	x₂	x₃	x₄	x₅	x₆
Probabilité	0.15	0.08	0.5	0.04	0.17	0.06