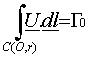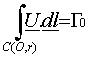Projet Scientifique

Les Cyclones Tropicaux

Matthieu ATTALI   Xavier CHASSAGNEUX   Lucien DÉGARDIN   Rodolphe GOURSEAU   Xavier MISSERI   Pierre-Louis NAUD  Ngoc Anh VU

31 mars 2003

  

Table des matières

1.  Dynamique bi-dimensionnelle

Pour comprendre certains comportements dynamiques des tourbillons atmosphériques, on utilise, en première approximation, un modèle simple appelé 2D-barotrope qui repose sur les approximations suivantes : En effet, en prenant comme grandeurs caractéristiques 1   L=106   m, U=50    m.s-1, n=10    m2.s-1, obtient un nombre de Reynolds Re~5.1012»1 et un nombre de Mach Mc~10-1«1, valeurs qui justifient respectivement les hypothèses du fluide inviscide et incompressible.

La hauteur caractéristique est  h=104   m et la longueur horizontale est  L=106   m   si bien que l'écoulement peut être considéré comme bi-dimensionnel dans le plan horizontal.
L'équation d'Euler à deux dimensions s'écrit alors :
U
t
+
grad
(
U
).
U
=
U
t
+
rot
(
U
)Ù
U
+
grad
(
U
2
2
) =-
grad
(p)
r

En passant cette équation au rotationnel, en utilisant l'incompressibilité du fluide 2, la définition 3 de w et en utilisant les formules sur les opérateurs vectoriels, on obtient :
D
w
D t
=
w
t
+
grad
(
w
).
U
=
grad
(
U
).
w
Mais, U est dans le plan horizontal, et w est selon ez, donc : grad(U).w=0 et on a alors :


D w/D t=0    (1.1)
Il y a donc conservation de la vorticité   w=( vy / x - vx/ y ) ez
L'écoulement étant incompressible, on a : div(U)=0. Donc : $ Y champ vectoriel tel que : U=rot(Y). De plus, l'écoulement étant bi-dimensionnel, on a : Y=Y(x,y) ez. Ainsi on a :
ì
ï
ï
í
ï
ï
î
vx=-
Y
y
vy=
Y
x
    (1.2)

  
On a alors : U.grad(Y)=vx Y/ x+vy Y/ y=vx vy-vy vx=0.
Ainsi : y=cteÞ dY=0Þgrad(Y).d l=0=grad(Y).UÞ     dl // U.
Donc les équi-Y correspondent aux lignes de courant. L'écoulement étant stationnaire, ce sont aussi les trajectoires.
Considérons un vortex ponctuel (w=0 sauf en r=0) de circulation G0. On a par conséquent 4:

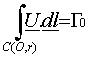
Or, par invariance par rotation 5 et par incompressibilité 6 de l'écoulement, U=U(r) eq et donc :
G0=2p r  U Þ U=
G0
2p r
D'où, à une constante près :


Y(r,q)=-(G0/2p)ln(r)    (1.3)

Un tel tourbillon est stationnaire et il est emporté par l'écoulement. Dans un écoulement à vitesse U, le tourbillon décrit une droite de même sens et de même direction 7 que U, à la vitesse U.

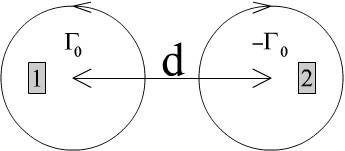
Figure 0.1 : Paire de vortex ponctuels de signe opposé (G0,-G0).

Dans le cas d'une paire de vortex, le vortex G0 induit une vitesse (G0/2p) d sur le vortex -G0, et le vortex -G0 induit une vitesse (G0/2p) d sur le vortex G0 (Fig.  0.1). Ainsi les deux tourbillons restent à la distance d et se déplacent à la vitesse (G0/2p) d vers le haut.

2.  Dynamique bi-dimensionnelle sur le globe


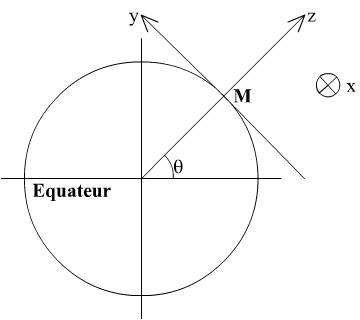
Figure 0.2 : Repère local utilisé dans la dynamique bi-dimensionnelle.

Afin de reproduire de certains effets dynamiques, il est nécessaire de prendre en compte la rotation de la Terre et la géométrie sphérique de celle-ci. On se place alors dans un repère localement cartésien en un point M de la surface du globe (Fig. 0.2).
Dans le référentiel galiléen géocentrique, il faut ajouter, à la vitesse relative de l'écoulement, la vitesse due à la rotation de la terre. Donc le rotationnel de la vitesse dans le référentiel est la somme de w et du rotationnel de la vitesse due à la rotation de la Terre, dont la projection sur l'axe vertical local 8 est deux fois le vecteur rotation 9. Cette projection vaut donc 2 W0sin(q). Ainsi on obtient :


D(w + f)/D t=0    (2.1)

f=2 W0sin(q)    (2.2)

Cependant, en coordonnées cartésiennes, les variations de f s'écrivent au premier ordre :


f~ 2W0sin(q) +(2W0cos(q)/R) y=f0+b y    (2.3)

L'approximation plan-beta est valide pour y/R infinitésimal 10.

b est maximal quand q= 0 c'est-à-dire à l'équateur.
Si on reprend l'équation (2.1), on obtient 11:
w
t
+
w
x
x
t
+
w
y
y
t
+
f
t
+
f
x
x
t
+
f
y
y
t
=0
Þ  
Y
t
+
Y
x
Y
y
-
Y
y
Y
x
+b
Y
x
=0

En notant J(f,g)=( f/ x)( g/ y)-( f/ y)( g/ x), on a :


Y/ t+J(Y,Y)+bY/ x=0    (2.4)
  
On considère alors un tourbillon axisymétrique 12 Y(x,y)=Y0(r). On a : J(Y0,Y0)=0 . En régime stationnaire, grâce à (2.3), on obtient :
bcos(q) 
Y0
r
=0
D'où, comme on ne veut pas une solution triviale et que b¹0:


q=±p/2    (2.5)
Un tourbillon axisymétrique stationnaire ne peut exister qu'aux pôles.
Un tourbillon aux latitudes tropicales peut, entraîné par la circulation atmosphérique à grande échelle, se déplacer en latitudes.
L'équation (2.1) donne w +f=cte. Or, quand le cyclone se déplace, f augmente et donc nécessairement w diminue. Ainsi, il existe une latitude où w s'annule et le cyclone disparaît alors.

3.  Trajectoire du cyclone

Pour calculer l'évolution initiale d'un tourbillon axisymétrique Y0(r) , on utilise un développement de Taylor de la fonction de courant :
Y(x,y,t)=Y0(r)+
t
t0
Y1(x,y)+(
t
t0
)2 Y2(x,y)+...
avec t0=1/b r0, r0 étant une taille caractéristique du tourbillon.
En utilisant l'équation (2.3), on obtient :
(Y)
t
=
Y1
t0
   en se plaçant à    t=0
J(Y,Y)=J(Y0,Y0)=0   (à  t=0)
De plus, à  t=0   
Y
x
=cos(q)
Y0
r
Et donc :


Y1/t0+b cos(q)Y0/ r=0     (3.1)

  
En choisissant un tourbillon initial défini par :
Y0(r)= ì
ï
ï
í
ï
ï
î
1
4
w0(r2-r02)
si r£ r0
1
6
w0 r02(1-(
r0
r
)3)
si r³ r0
on obtient, en résolvant l'équation (3.1) 13:
Y1(r)= ì
ï
ï
í
ï
ï
î
cos(q)(
w0 r0 r
6
+
w0 r3
16r0
)
si r£ r0
-cos(q)(
w0 r04
3r2
+
w0 r03
12r
)
si r³ r0
     (3.2)
Donc au centre du tourbillon, la vitesse induite par Y1 est :
ì
ï
ï
í
ï
ï
î
vx(r=0)=-
Y1
y
(r=0)=0
vy(r=0)=
Y1
x
(r=0)=
w0 r0
6
soit


v(r=0)=w0 r0/6 ey     (3.3)

  
Ainsi, le cyclone va se déplacer selon ey, c'est-à-dire vers le nord dans l'hémisphère nord et vers le sud dans l'hémisphère sud (b<0 dans l'hémisphère sud).

Plus précisément, en raisonnant dans l'hémisphère nord, Y1 est un dipôle et Y0 fait tourner ce dipôle. Dons juste après sa formation, le cyclone va se diriger vers le nord avec une courbure vers l'ouest due à la force de Coriolis. Mais le temps t augmentant, la contribution amenée par y1 va devenir prépondérante si bien que le cyclone va dévier vers l'est 14 jusqu'à ce que le cyclone disparaisse.

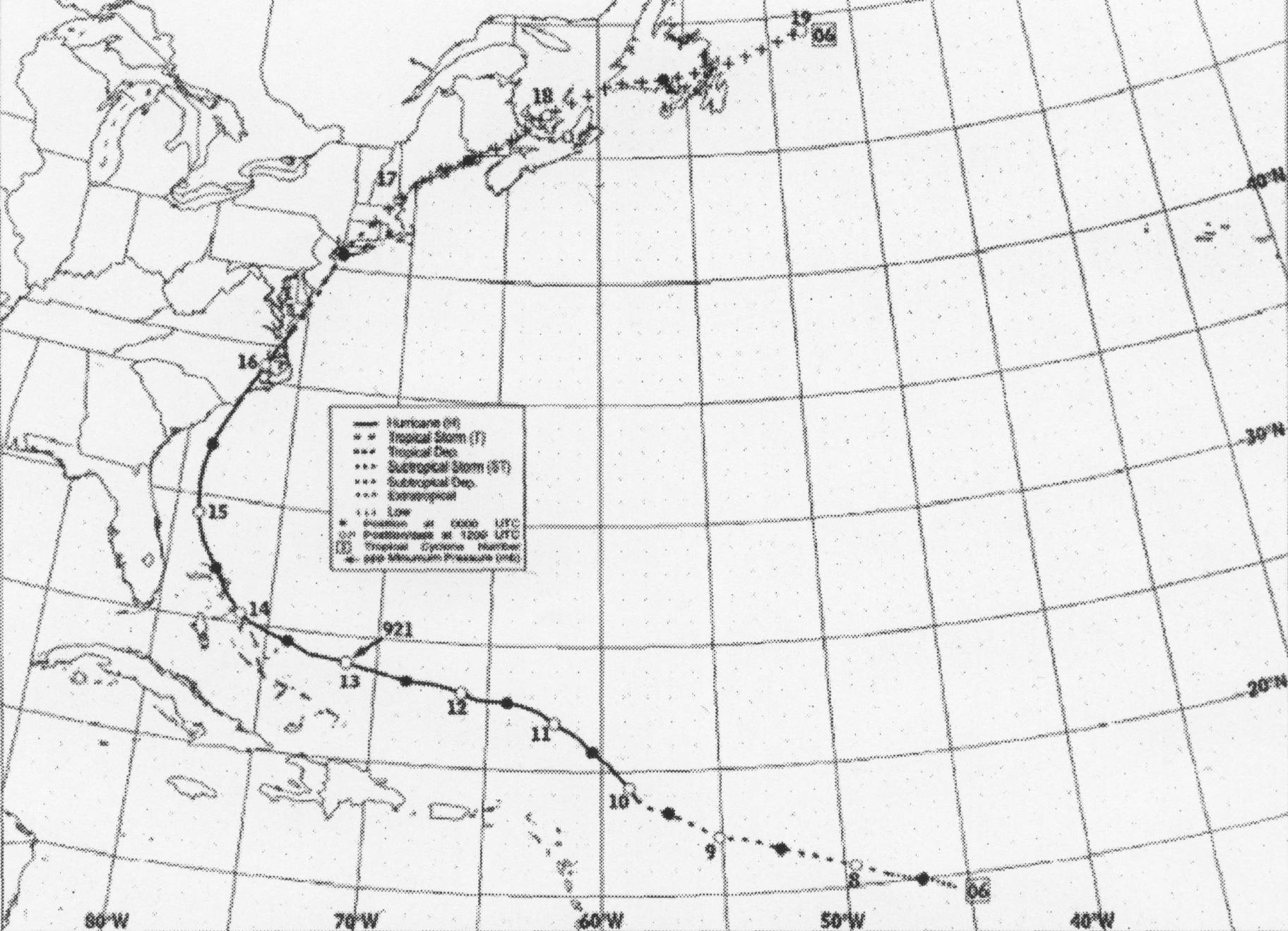
Figure 0.3 : Best track positions for Hurricane Floyd, 07-17 September 1999.

L' exemple du cyclone Floyd (Fig.  0.3) montre bien le déplacement bien vers le nord pour l'hémisphère nord.   
Le modèle est "très loin" de prédire la trajectoire réelle d'un cyclone car il utilise le plan tangent pour le déplacement. Ceci n'est valable qu'au premier ordre. Le modèle ne tient en plus pas compte ni des vents ni du relief qui sont des éléments non négligeables dans la trajectoire des cyclones.
1
 grandeurs caractéristiques pour des tourbillons atmosphériques tels des cyclones, des dépressions, et des anticyclones
2
 div(U)=0 et r=cte
3
  w=rot(U)=w  ez   car écoulement bi-dimensionnel
4
 où C(O,r) est le cercle de centre O et de rayon r>0
5
 U=U(r)
6
 div(U)=0Þ(r Ur)/ r=0Þ Ur=A/r¾®r® 00Þ A=0Þ U=U(q)eq
7
 théorème de Helmholtz
8
 on ne s'intéresse pas aux autres composantes ici puisque l'écoulement est supposé bi-dimensionnel
9
 la vorticité dans une rotation solide vaut deux fois le vecteur rotation
10
 donc pour des valeurs de y inférieures à 500   km
11
 en utilisant le fait que : $ Y;  U=rot(Yez) Þ w=rot(rot(Y))=grad(div(Y))-DY et div(Y)=0
12
 tourbillon à symétrie cylindrique qui en première approximation rend compte de l'écoulement d'un cyclone
13
 les constantes sont fixées par continuité du champ et de sa dérivée car U est continue
14
 le pôle le plus au nord du dipôle est plus intense que le pôle le plus au sud
Ce document a été traduit de LATEX par HEVEA.